【注意】ここに書いてあることは,心理学専攻の大学学部生向けの情報です。他の分野にはあてはまらないこともあります。
- Excelの「データ分析」が見つかりません
- Excelの「データ分析」のt検定がいろいろあってよくわかりません
- p値が「5.10213E-12」のように表示されるのですが,どういう意味ですか
- Excelでz値,t値,F値,χ2値からp値を求める方法を教えてください
- Excelのt検定の結果の見方がわかりません
- p値の論文での書き方がわかりません
- レポートや論文での検定結果の書き方がわかりません
- 例題の計算結果が解答と微妙に一致しません。なぜでしょうか
- z検定やt検定には両側検定と片側検定がありますが,どう使い分けたらよいのですか
- Excelでできない検定や分析はどうしたらよいのですか
- Excelの「データ分析」が見つかりません
- Excelの「データ分析」のt検定がいろいろあってよくわかりません
- p値が「5.10213E-12」のように表示されるのですが,どういう意味ですか
- Excelでz値,t値,F値,χ2値からp値を求める方法を教えてください
- Excelのt検定の結果の見方がわかりません
- p値の論文での書き方がわかりません
- レポートや論文での検定結果の書き方がわかりません
- 例題の計算結果が解答と微妙に一致しません。なぜでしょうか
- z検定やt検定には両側検定と片側検定がありますが,どう使い分けたらよいのですか
- Excelでできない検定や分析はどうしたらよいのですか
分析ツールのアドインを追加して下さい。ファイル→オプション→アドイン あたりです。Microsoftのヘルプを参照のこと
なお,t検定などを行う「データ分析」は,「ホーム」の「データ分析」ではなく,「データ」の「データ分析」です
「t検定: 一対の標本による平均の検定」→ いわゆる対応のあるt検定。対応のある2つの群(条件)の平均値に差があるかどうか。『テクニカルブック』pp. 65-68,『よくわかる心理統計』pp. 150-153
「t検定: 等分散を仮定した2標本による検定」→ いわゆる対応のないt検定(対応のない,独立な2つの群(条件)の平均値に差があるかどうか)で,両群の分散が等質であると仮定した場合。『テクニカルブック』pp. 60-63,『よくわかる心理統計』pp. 146-149
「t検定: 分散が等しくないと仮定した2標本による検定」→ いわゆる対応のないt検定で,両群の分散の等質性を仮定しない場合。Excelのこの項目はウェルチの検定を実行しますが,自由度は四捨五入した整数値が返されるようです(p値もこの四捨五入した値に基づいて計算されます)。多くのテキストでは,切捨てた整数値で検定を行うことを推奨していますので(誤って有意差ありと結論してしまう可能性を減らすため),p値がぎりぎり有意水準近くだった場合には注意してください。『テクニカルブック』pp. 64-65,『よくわかる心理統計』pp. 154-157
分析ツールのMicrosoftヘルプも参照のこと
5.10213 × 10-12 という意味です。つまり 0.00000000000510213 です。Eは指数(exponential)のこと。0.001を下回るようなとても小さなp値は,論文では p < .001 と書いておけばOK。Eのついたまま書くのはやめましょう。
z値からp値(両側確率)を求めるには,下のようにします。Excel関数norm.s.dist(z値,true)は両側確率ではなく下側確率を返すことに注意。absは絶対値を求める関数。
=(1-norm.s.dist(abs(z値),true))*2
t値からp値(両側確率)を求めるには,下のようにします。t.dist.2t関数はt値として負の値を指定するとエラーになります(ので,abs関数をつけています)。
=t.dist.2t(abs(t値),自由度)
分散分析のF値からp値(F分布の上側確率)を求めるには,下のようにします。F値が負になることはありません。2つの自由度の順番を逆にしないよう注意。F(2, 6) = 1.23 なら,=f.dist.rt(1.23,2,6) です。
=f.dist.rt(F値,分子の自由度,分母(誤差項)の自由度)
χ2(カイじじょう)値からp値(χ2分布の上側確率)を求めるには,下のようにします。χ2値も負にはなりません。
=chisq.dist.rt(χ2値,自由度)
z, t, F, χ2などの値は四捨五入したものを手打ち入力するのではなく,=t.dist.2t(abs(G23),G24) のようにセルを直接参照して代入しましょう(丸めの誤差を減らすため)。
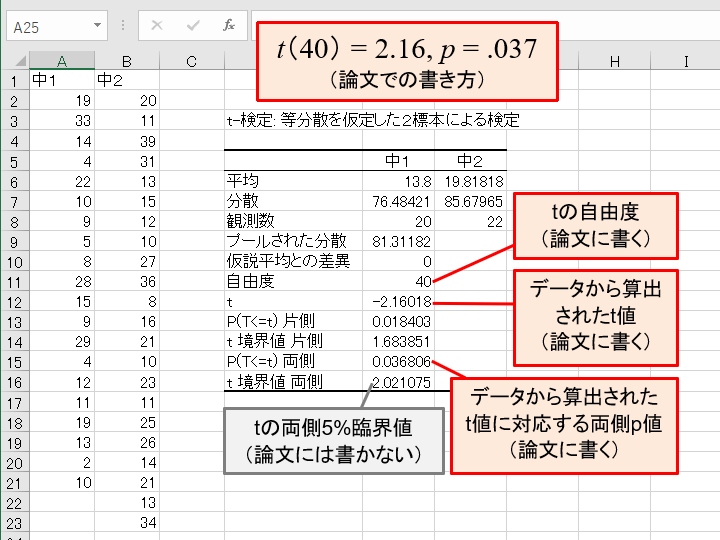
上の例では両側検定なので,「P(T<=t)両側」が有意水準より小さければ有意差ありです。論文では,両側検定の場合,t値のマイナスは省略して書くことが多いです。数値は適切な桁数に四捨五入して書きましょう。
検定結果のp値は,有意水準と比べた不等号で書く方法(p < .05 とか p > .10)と,具体的なp値を書く方法(p = .037 とか p = .234)がありますが,後者がおすすめです(情報量が多いから)。前者のような不等号による表記は,コンピュータが普及しておらずp値を求めるのが非常に難しかった時代のなごりです。
ただし,p値が非常に小さく0.001(0.1%)を下回る場合には, p < .001と書くのが普通です。また,図表では不等号による表記をよく使います。
p値を書くときは,小数点以下3ケタ程度に四捨五入して書くのが一般的です。また,p値は絶対に1を越えないので,小数点の左のゼロはよく略されます(APAスタイルでは略します)。有意水準が5%だという意味でp = .05と書くのはやめましょう。誤解のもとです。有意水準は言葉で明記する(「有意水準5%で検定を行ったところ,……」)か,ギリシャ文字のアルファを使ってα = .05と表します。
『心理学研究』に載っている論文の書き方をまねしてください。ただし,新しい論文を参考にすること。検索ではいろいろな学会抄録や卒論なども出てきますが,プロが校正していない場合が多いので,書式の参考にはしない方がいいです。
レポートの書式テンプレや,「心理学論文における数値と統計の書き方」も参考にしてください。日本心理学会の「執筆・投稿の手びき」や,APAマニュアル(日本語訳が出版されています)も参考になります。
表記法が定まっていないケースもありますが,大切なのは「正確でわかりやすい」表記法が「一貫して」用いられていることです。迷ったら,最も適切だと思う表記法を自分で選んで,レポート・論文内では一貫してその表記法を使ってください。
なお,実習レポートなどでは統計の勉強のために論文では書かないような詳しい情報(途中計算過程など)を書くように指示される場合があります。その場合は,指示に従ってください。たとえば,実際の論文では分散分析表はめったに載せませんが,統計の授業レポートでは分散分析表を書けと言われることがあります。
論文に検定結果を書くときのよくある注意事項をいくつか挙げておきます。
検定結果は言葉で説明し,数値はカッコ内にオマケとしてつける。
× t検定の結果,t(40) = 2.16, p = .037だった。
○ t検定の結果,有意差があった(t(40) = 2.16, p = .037)。
◎ t検定の結果,学習条件の正答率は統制条件より有意に高かった(t(40) = 2.16, p = .037)。
半角コンマの後,イコールの前後など必要な場所に半角スペースを入れる。
× ……が有意に高かった(t(40)=2.16,p=.037)。
○ ……が有意に高かった(t(40) = 2.16, p = .037)。
コンマを含む検定結果を列挙したいときは,半角セミコロン(;)で区切る。これは,コンマを含む語句を列挙するときにセミコロンで区切る英語の一般的な表記法に従ったものです。セミコロンは全角でははなく半角です。半角セミコロンの前にはスペースを入れません。半角セミコロンの後には半角スペースを入れます。
△ ……いずれの主効果も有意ではなかった(表情,F(2, 22) = 0.68, p = .517, 色,F(1, 11) = 2.71, p = .128)。
○ ……いずれの主効果も有意ではなかった(表情,F(2, 22) = 0.68, p = .517; 色,F(1, 11) = 2.71, p = .128)。
○ ……表情と色のいずれの主効果も有意ではなかった(それぞれ,F(2, 22) = 0.68, p = .517; F(1, 11) = 2.71, p = .128)。
計算途中で四捨五入していませんか(たとえば20÷3=6.6666...を6.67とする,など)。計算途中で四捨五入すると,計算誤差が増えます。これを丸めの誤差と言います。計算途中での手動の四捨五入は一切行わず,すべてExcel任せで計算しましょう。
なお,データや検定結果を論文に書く時には,適切な桁数に四捨五入して書きます。つまり,四捨五入は,最後に論文に書く時にだけ行うのがふつうです。
厳密に言えば,Excelなどのコンピュータソフトも四捨五入しながらデータを計算していますが,人間が紙で行う手計算よりずっと多い桁数で計算しているので,計算精度が高いのです。高校数学ではあまり意識しないかも知れませんが,現実のデータの計算には常に誤差がつきまとうということに注意しましょう。実験・調査データを扱う際には誤差や精度を意識することが必要です。
とりえあず,デフォルトは両側検定だと思っておいてください。片側検定は(少なくとも心理学の一般的な研究では)あまり使いません。論文でも,両側検定であることをあえて明記することは少ないですが,片側検定を使った場合は明記し,理由も述べるのが普通です。
両側検定か片側検定かは,実験計画の一部として事前に決めておくのが原則です。事前に,です。実験結果や調査結果を見てから片側検定か両側検定かを決めたり,片側検定の方向性を決めたりするのはNGです。得られた結果に従って検定手法を都合よく変えることは統計的仮説検定のロジックに矛盾します。
多くの場合,研究者の持っている仮説には方向性があります。従来の学習法を用いた統制群に比べて,新開発の学習法を使った実験群は成績が「高い」だろう,というように。それでも「高いかどうか」(片側検定)ではなく「差があるかどうか」(両側検定)を検定する場合がほとんどです。なぜなら,研究者の仮説に反して実験群の成績の方が低くなってしまう可能性も十分に考えられるからです(新しい学習法には未知の欠点があった,慣れない学習法のため強い疲労効果が生じてしまった,個人差,予想外の交絡変数……)。実際の結果がどうなるかは,実験してみないとわかりません(だから実験するのです!)。そして片側検定では,予想と逆向きの差があったかなかったか結論することができません。両側検定ならば,逆向きの差についても有意差があったかどうか言うことができるので,たとえば「予想に反する方向の差だが有意だったので,未知の要因がひそんでいる可能性がある」とか,「有意差がないので,新しい学習法が有益であるとは結論できないが,少なくとも従来の学習法より劣ってもいない」とか,いろいろな考察ができます。
簡単な検定で,データ量も多くないなら,Excel上で手動計算しましょう。sum(合計),average(平均),stdev.s(標準偏差の不偏推定値),stdev.p(母集団の標準偏差),correl(相関係数),sqrt(平方根),abs(絶対値),count(数値データの個数),if(条件分岐)などのExcel関数を活用してください。「データ」→「並べ替え」や,条件に合致するデータのみの平均を求めるaverageifなども便利です。
二項検定は,二項分布の確率を求めるExcel関数binom.distを使えばできます。一次回帰は「データ分析」→「回帰分析」です。
それ以外のいろいろな分析には,より統計に特化したソフトが必要です。JASPはマウス操作でいろいろな分析ができ,ベイズファクターの算出などベイズ的な分析も可能です。jamoviも同様です。ブラウザで動作するものとしてはjs-STARがあります。心理系大学生向けのExcel上で動作する統計分析ソフトとしてHADがあります。
大学院進学を目指すなど,本格的に統計を使いたいなら,ぜひR(アール)を使ってみましょう。多数のパッケージ(追加機能のようなもの)が開発されており,専門的な分析もできます。プログラミングによるデータの集計,グラフなどデータの可視化もできるので,慣れれば非常に便利です。詳しくはRjpWikiなどを参照。本もたくさん出ています。Rを使いやすくしたものに,RStudioがあります。Rで分散分析を行う場合,ANOVA君も便利です。
Mathworks社のMATLABでも,さまざまな統計分析ができます。グラフ作成などのデータ可視化も高機能です。新潟大学はCampus Wide Licenseを導入しているので,在学中は無償で利用できます(個人PCへのインストールも可)。詳しくは情報基盤センターのHPを見て下さい(詳細な情報は学内ネットワークからでないと見られないかもしれません)。なお,MATLAB本体に加えてStatistics and Machine Learning Toolboxもインストールしておくとよいでしょう。